Finding the radius of convergence. Hence the radius of convergence is R 3.

Find The Radius Of Convergence Of The Power Series Sum 1 Nx N N 1 Convergence Math Videos Power Series
Has a radius of convergence R 1 limsup n p ja nj.
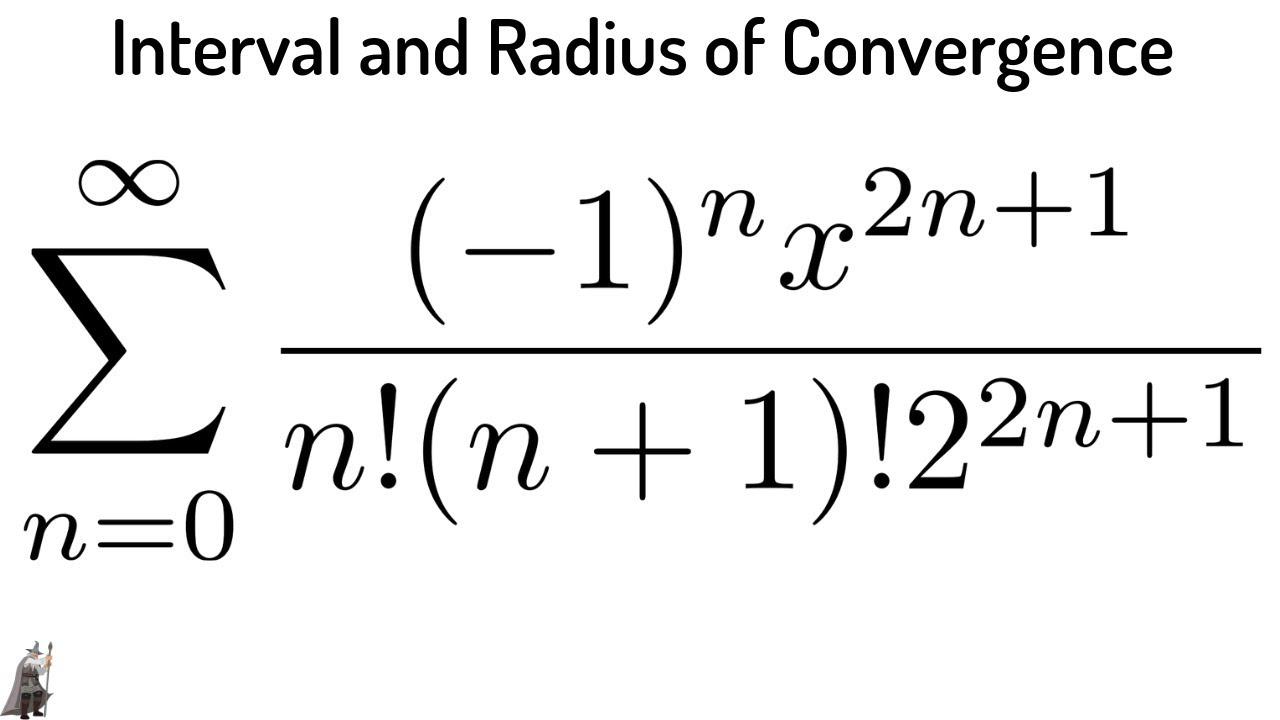
. Assuming x 0 2R the distance to each is the same so lets compute the distance to i. The radius of convergence R is any number such that the power series will converge for x a R and diverge for x a R. Radius of Convergence of Series.
For the above power series when we put x 0 the series calculates to 1 0 0 0 0. X n0 1n x 3n 2n 1 8. X n1 10nxn n3 5.
Radius of Convergence Reiterating the main result to be shown in this writeup any given complex power series fz X1 n0 a nz cn. Thus the interval of convergence is 33 and the radius of convergence is R 3. X n0 1nxn n 1 2.
Again the result is that fz converges absolutely on the open disk of radius R about c and this convergence is uniform on compacta but fz diverges if. In this video we learn about how to find the radius of Convergence of a power series. N 0 c n x a n.
It is called a radius because we often consid. This distance is jx 0 ij p x2 0 1. However we can come close.
For x 1 the series of partial sums no longer converges. Free Radius of Convergence calculator - Find power series radius of convergence step-by-step This website uses cookies to ensure you get the best experience. If the power series only converges for x a then the radius of convergence is R 0 and the interval of convergence is x a.
We look at the distance between x 0 and these singularies. If there is no nonzero real number for which the power series. The radius of convergence is usually the distance to the nearest point where the function blows up or gets weird.
X n1 x n 5nn5 6. The second case is practical. And converges at 1 and does not exceed the series beyond 1 as it will make the series divergent.
By using this website you agree to our Cookie Policy. The power series may not converge for x a R. Likewise if the power series converges for every x the radius of convergence is R infty and interval of convergence is -.
If a then a x a c and because c is a constant the series cannot converge with the exception of c 0. When you know all the coefficients then you take certain limits and find the precise radius of convergence. If the radius of convergence of the power series sum_n 0infty c_n xn is 10 what is the radius of convergence of the series sum_n 1infty nc_n xn -1.
The radius of convergence is infinite if the series converges for all complex numbers z. Zero radius of convergence. If the series only converges at a single point the radius of convergence is 0.
The expression 1 x x2 x3. By taking the square-root x 4 3 R. In this problem we need to determine the radius of convergence of a given series.
X n1 nnxn 4. However the online radius and interval of convergence calculator finds the range of series for which it converges. Radius of convergence is 10.
Thus the radius of convergence is 0. In the latter case we call r the radius of convergence of the power series n 0anxn. The singularities of f are where 1 x2 0 ie.
Practice Problems Determine the interval of convergence of the following power series. So from here we can determine that the NFL films E N is equal to end times actually Power End also A of N plus one will be obtained by replacing and by N plus one and we will get 10 plus one. If x 0 2 the radius of convergence is p 5 so converges in 2.
If the radius of convergence of the power series sigma_i0infinity c_nyn is 17 what is the radius of convergence of the series sigma_i1infinity nc_nyn-1 34 0. The distance between the center of a power series interval of convergence and its endpoints. The radius of convergence is usually the distance to the nearest point where the function blows up or gets weird.
Thus the radius of convergence for this series is 1. If the series converges over all real numbers the radius of convergence is. By multiplying by 3 x 42 3.
Answer 1 of 5. The convergence of the infinite series at X-1 is spoiled because of a problem far away at X1 which happens to be at the same distance from zero. In our example the center of the power series is 0 the interval of convergence is the interval from -1 to 1 note the vagueness about the end points of the interval its length is 2 so the radius of convergence equals 1.
If a 0 then a x a c 0 and because c is a constant the series converges for all values of c. The convergence of the infinite series at X-1 is spoiled because of a problem far away at X1 which happens to be at the same distance from zero. It is customary to call half the length of the interval of convergence the radius of convergence of the power series.
X n0 1n x2n 2n. X n1 3x 2 n3n 10. In the former case we say that the radius of convergence of n 0anxn is.
Though we can say that n 0anxn converges absolutely when x r we cannot say that the convergence is uniform. X n1 n 4n x 1n 9. Consider the power series.
When you construct a power series solution of a difficult problem you. Calculus 2 BC. Converges for all values of x 1.
The first case is theoretical. Consider a simple example. X n1 nxn 3.
Now this problem the given series is summation and is equal to 02 infinity end times actually power in. So if x 0 0 the radius of convergence of the above series is 01 1. This video is very helpful for various Competitive Exams such as mast.

Radius Of Convergence Kristakingmath Youtube

Find The Interval Of Convergence For The Power Series Sum 1 Nn X Math Lessons Convergence Math Videos
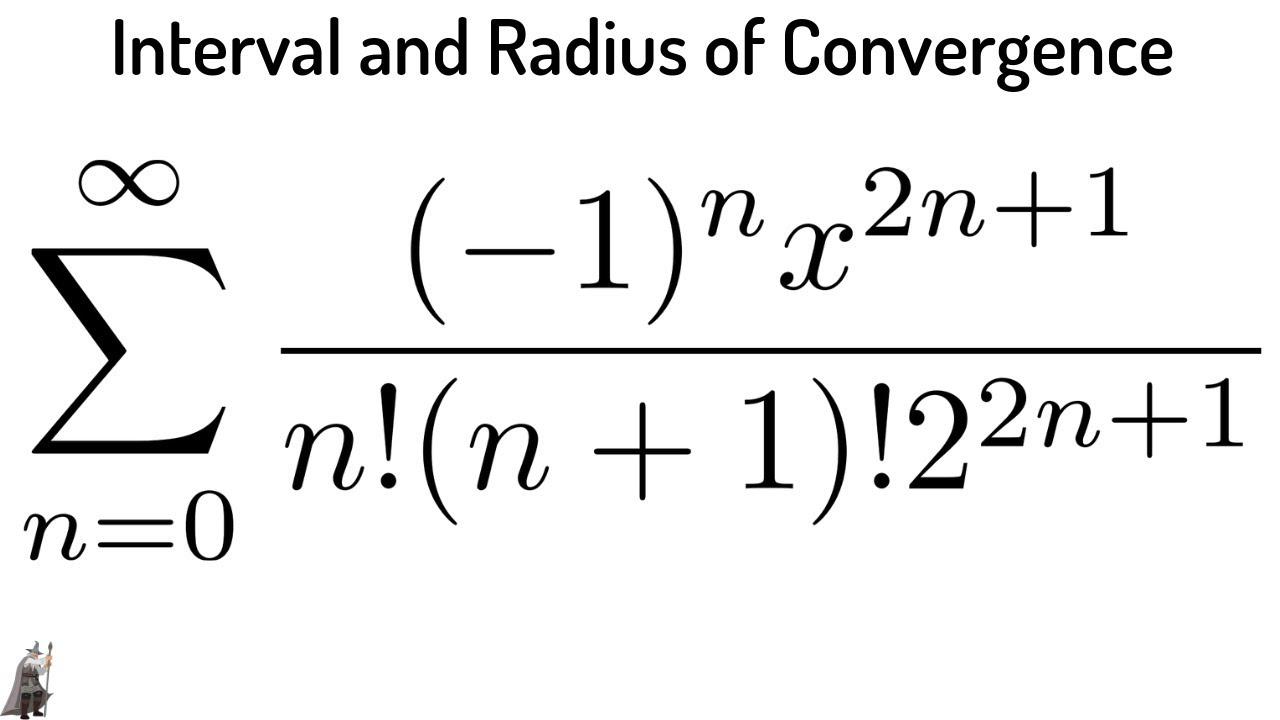
Interval And Radius Of Convergence A Power Series Using The Ratio Test F Convergence Math Videos Calculus
0 Comments